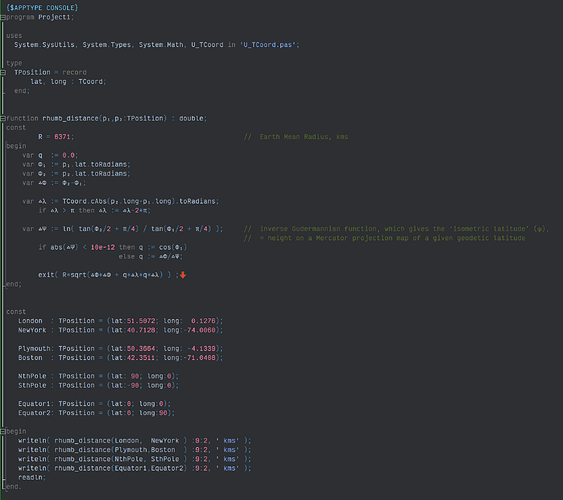
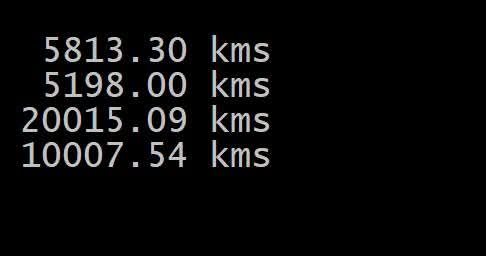
If you are interested in Rhumb Distrance in Delphi
function RNavigateLongLat.MetresFrom(AStart: RNavigateLongLat): Double;
{ https://www.movable-type.co.uk/scripts/latlong.html
Haversine
formula: a = sin²(Δφ/2) + cos φ1 ⋅ cos φ2 ⋅ sin²(Δλ/2)
c = 2 ⋅ atan2( √a, √(1−a) )
d = R ⋅ c
where φ is latitude, λ is longitude, R is earth’s radius (mean radius = 6,371km);
note that angles need to be in radians to pass to trig functions!
JavaScript:
var R = 6371e3; // metres
var φ1 = lat1.toRadians();
var φ2 = lat2.toRadians();
var Δφ = (lat2-lat1).toRadians();
var Δλ = (lon2-lon1).toRadians();
var a = Math.sin(Δφ/2) * Math.sin(Δφ/2) +
Math.cos(φ1) * Math.cos(φ2) *
Math.sin(Δλ/2) * Math.sin(Δλ/2);
var c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1-a));
var d = R * c;
Also http://www.reeve.com/Documents/Articles%20Papers/Reeve_PosDistBrngCalcs.pdf
}
Var
DeltaLong, DeltaLat, a, b, c: Double;
begin
if not(IsValid and AStart.IsValid) then
begin
Result := 0.0;
Exit
end;
DeltaLong := LongitudeRad - AStart.LongitudeRad; // Δλ
DeltaLat := LatitudeRad - AStart.LatitudeRad; // Δφ
a := sin(DeltaLat / 2);
b := sin(DeltaLong / 2);
a := a * a + Cos(AStart.LatitudeRad) * Cos(LatitudeRad) * b * b;
c := 2 * ArcTan2(Sqrt(a), Sqrt(1 - a));
Result := EarthRad * c;
end;
function RNavigateLongLat.MetresFromPrecision(AStart: RNavigateLongLat;
out ARadiansToStart, ARadiansFromStart: Double; AAllowPolarRoute: Boolean): Double;
// https://www.movable-type.co.uk/scripts/latlong-vincenty.html
// Semi-major axis a = 6378137.0 metres
// Semi-minor axis b ≈ 6356752.314245 metres
// Inverse flattening 1/f = 298.257223563
Const
MjrAxis = 6378137.0; // Metres
MnrAxis = 6356752.314245;
PolarElipseSemiGa = 20003931.458;
// From www.ga.gov.au/geodesy/datums/vincenty_inverse.jsp
var
FinalBearing:Double;
Flat, TanLat1Adj, CosLat1Adj, SinLat1Adj: Extended;
SpecialCaseAdj: RNavigateLongLat;
TanLat2Adj, CosLat2Adj, SinLat2Adj, SinLatAdjMult, CosLatAdjMult: Extended;
DeltaLong, Lamda, LamdaDash, Sigma: Extended;
SinLamda, CosLamda, SinSqSigma, SinSigma, CosSigma, PolarElipseSemi, EqaSemi,
SqVal: Extended;
SinAlpha, CosSqAlpha, Cos2SigmaM, Cos2SigmaMSq, DeltaSigma, c, uSq, AVal,
BVal, TstComplete, Result2: Extended;
InterateLim: Integer;
AZEqFwd, AzEqRev, SpecialCaseLongitude: Double;
Done: Boolean;
begin
Flat := (MjrAxis - MnrAxis) / MjrAxis;
DeltaLong := LongitudeRad - AStart.LongitudeRad;
if SameValue(LatitudeRad, -AStart.LatitudeRad, 0.25) then
// 80, -5, 260, 4.78, Failed to Converge
if AAllowPolarRoute then
Begin
if SameValue(Abs(DeltaLong), Pi,
0.0105331658 { 23' 47.3" 36 / 60 * pi / 180 } ) then
// 90+47/60, 0, 270,0, Failed to Converge
if ((LatitudeRad < 40 / 180 * Pi) and (LatitudeRad > -40 / 180 * Pi))
then
// 80, -40, 260, 40, Converged
begin
SpecialCaseAdj.Create(LongitudeRad, -AStart.LatitudeRad);
// PolarElipseSemi := pi * Sqrt((MjrAxis * MjrAxis + MnrAxis * MnrAxis) / 2);
// EqaSemi := pi * MjrAxis;
// Special Case over the pole
Result := MetresFromPrecision(SpecialCaseAdj, ARadiansToStart, ARadiansFromStart);
Result := PolarElipseSemiGa - Result;
ARadiansToStart := Pi;
ARadiansFromStart := Pi;
if LatitudeRad < -AStart.LongitudeRad then
Begin // end closer to equator
if LatitudeRad < 0 then
ARadiansFromStart := 0
Else
ARadiansToStart := 0;
End
Else // Start closer to equator
if LatitudeRad > 0 then
ARadiansFromStart := 0
Else
ARadiansToStart := 0;
Exit;
end;
End
else if SameValue(Abs(DeltaLong), Pi, 0.01 * Pi) then
// Solution over a wider range as uses mid point on equater
if ((LatitudeRad < 40 / 180 * Pi) and (LatitudeRad > -40 / 180 * Pi)) then
// 80, -40, 260, 40, Converged
begin
// Split into two arround equiltorial mid piont
SpecialCaseLongitude := (LongitudeRad + AStart.LongitudeRad) / 2;
SpecialCaseAdj.Create(SpecialCaseLongitude, 0);
Result := MetresFromPrecision(SpecialCaseAdj, AZEqFwd, ARadiansFromStart, false);
Result2 := SpecialCaseAdj.MetresFromPrecision(AStart, ARadiansToStart,
AzEqRev, false);
Result := Result + Result2;
Exit;
end;
TanLat1Adj := (1 - Flat) * Tan(AStart.LatitudeRad);
CosLat1Adj := 1 / Sqrt(1 + TanLat1Adj * TanLat1Adj);
SinLat1Adj := TanLat1Adj * CosLat1Adj;
TanLat2Adj := (1 - Flat) * Tan(LatitudeRad);
CosLat2Adj := 1 / Sqrt(1 + TanLat2Adj * TanLat2Adj);
SinLat2Adj := TanLat2Adj * CosLat2Adj;
SinLatAdjMult := SinLat1Adj * SinLat2Adj;
CosLatAdjMult := CosLat1Adj * CosLat2Adj;
// Only for warnings
Cos2SigmaM := 0.0;
SinLamda := 0.0;
SinSigma := 0.0;
CosSqAlpha := 0.0;
CosLamda := 0.0;
CosSigma := 0.0;
SinSqSigma := 0.0;
Sigma := 0.0;
// Only for warnings
Lamda := DeltaLong;
TstComplete := Lamda * 0.000001;
Done := false;
InterateLim := 100;
while Not Done and (InterateLim > 0) do
begin
SinLamda := sin(Lamda);
CosLamda := Cos(Lamda);
SqVal := (CosLat1Adj * SinLat2Adj - SinLat1Adj * CosLat2Adj * CosLamda);
SqVal := SqVal * SqVal;
SinSqSigma := CosLat2Adj * SinLamda * CosLat2Adj * SinLamda + SqVal;
SinSigma := Sqrt(SinSqSigma);
Done := SameValue(SinSigma, 0.0, 0);
if Done then
begin // Coincident points
Result := 0.0;
ARadiansToStart := 0.0;
ARadiansFromStart := 0.0;
Exit;
end
Else
begin
CosSigma := SinLatAdjMult + CosLatAdjMult * CosLamda;
Sigma := ArcTan2(SinSigma, CosSigma);
SinAlpha := CosLatAdjMult * SinLamda / SinSigma;
CosSqAlpha := 1 - SinAlpha * SinAlpha;
if SameValue(CosSqAlpha, EqualsValue, 0) then
Cos2SigmaM := 0.0
else
Cos2SigmaM := CosSigma - 2 * SinLatAdjMult / CosSqAlpha;
if IsNan(Cos2SigmaM) then
Cos2SigmaM := 0.0; // Equitorial Line
c := Flat / 16 * CosSqAlpha * (4 + Flat + +(4 - 3 * CosSqAlpha));
LamdaDash := Lamda;
Lamda := DeltaLong + (1 - c) * Flat * SinAlpha *
(Sigma + c * SinSigma * (Cos2SigmaM + c * CosSigma *
(-1 + Cos2SigmaM * Cos2SigmaM)));
Done := SameValue(Lamda, LamdaDash, 0.0);
end;
Dec(InterateLim);
end;
if Not Done then
raise Exception.Create('MetresFromPrecision Failed to Converge');
uSq := CosSqAlpha * (MjrAxis * MjrAxis - MnrAxis * MnrAxis) /
(MnrAxis * MnrAxis);
AVal := 1 + uSq / 16384 * (4096 + uSq * (-768 + uSq * (320 - 175 * uSq)));
BVal := uSq / 1024 * (256 + uSq * (-128 + uSq * (74 - 47 * uSq)));
Cos2SigmaMSq := Cos2SigmaM * Cos2SigmaM;
DeltaSigma := BVal * SinSigma *
(Cos2SigmaM + BVal / 4 * (CosSigma * (-1 + 2 * Cos2SigmaMSq) - BVal / 6 *
Cos2SigmaM * (-3 + 4 * SinSqSigma) * (-3 + 4 * Cos2SigmaMSq)));
Result := MnrAxis * AVal * (Sigma - DeltaSigma);
ARadiansToStart := ArcTan2(CosLat2Adj * SinLamda,
(CosLat1Adj * SinLat2Adj - SinLat1Adj * CosLat2Adj * CosLamda));
if ARadiansToStart < 0 then
ARadiansToStart := ARadiansToStart + 2 * Pi;
FinalBearing := ArcTan2(CosLat1Adj * SinLamda,
(-SinLat1Adj * CosLat2Adj + CosLat1Adj * SinLat2Adj * CosLamda));
ARadiansFromStart:=FinalBearing-Pi;
While ARadiansFromStart < 0 Do
ARadiansFromStart := ARadiansFromStart + 2 * Pi;
end;
Has the added advantage that it attempts to address the case where the start and end are on the opposite side of the globe.
RNavigateLongLat is a record
RNavigateLongLat = record
Private
LongitudeRad, LatitudeRad: Double;
LongitudeDec, LatitudeDec: Double;
........
The full record code is available from Delphi-Navigation-And-Sensors/LibraryCode at main · rogerinnova/Delphi-Navigation-And-Sensors · GitHub File ISNav Utils.pas