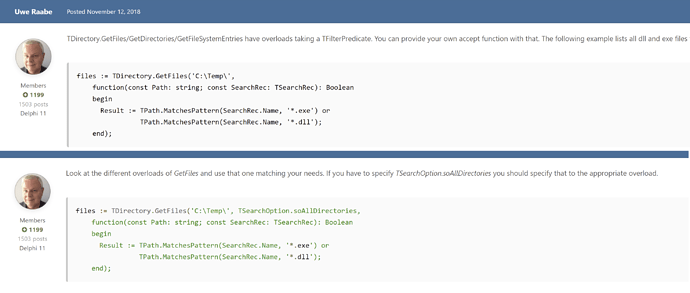
Using an anonymous selection predicate (boolean lambda function) with TDirectory.GetFiles …
(2012) Why LINQ Matters: Cloud Composability Guaranteed
By Brian Beckman - Communications of the ACM
“LINQ borrowed its essential concepts … from Haskell, specifically from its initialization library called Prelude.”
"LINQ’s foundation is the monad type class borrowed from the Haskell programming language. A monad is an interface for managing monoidal container structures, including lists, sets, bags, and permutations. LINQ does not presuppose or guarantee order. No matter how one might linearize a graph into, say, an ordered list or unordered bag, LINQ will not change the given order.
As for convolutions, continuations, and exceptions, I need only show that a collection is monadic to show it is also LINQable. For convolutions, under the Fourier representation, LINQ operates on vector spaces, which are monads. For the continuation and exception monads (called the Maybe monad), see Haskell documentation http://www.haskell.org/haskellwiki/Haskell."
Ian Boyd. StackOverflow. 2017.

(<0) // 4: Haskell
_ < 0 // 5: Scala
_1 < 0 // 6: Boost.Lambda
#(< % 0) // 8: Clojure
&(&1 < 0) // 9: Elixir
|e| e < 0 // 9: Rust
\(e) e < 0 // 10: R 4.1
{ $0 < 0 } // 10: Swift
{ it < 0 } // 10: Kotlin
e -> e < 0 // 10: Java
e => e < 0 // 10: C#, JS, Scala
\e -> e < 0 // 11: Haskell
{ |e| e < 0 } // 13: Ruby
{ e in e < 0 } // 14: Swift
{ e -> e < 0 } // 14: Kotlin
fun e -> e < 0 // 14: F#, OCaml
lambda e: e < 0 // 15: Python
(λ (x) (< x 0)) // 15: Racket
fn x -> x < 0 end // 17: Elixir
(lambda (x) (< x 0)) // 20: Racket/Scheme/LISP
[](auto e) { return e < 0; } // 28: C++
std::bind(std::less{}, _1, 0) // 29: C++
func(e int) bool { return e < 0 } // 33: Go
function(e: Integer): Boolean begin exit(e < 0) end // 51: Delphi [edited]
function(e: Integer): Boolean begin Result := e < 0 end // 55: Delphi
![]()
Rust …
// Imperative approach
fn is_odd(n: u32) -> bool {
n % 2 == 1
}
fn main() {
println!("Find the sum of all the squared odd numbers under 1000");
let upper = 1000;
// Declare accumulator variable
let mut acc = 0;
// Iterate: 0, 1, 2, ... to infinity
for n in 0.. {
// Square the number
let n_squared = n * n;
if n_squared >= upper {
// Break loop if exceeded the upper limit
break;
} else if is_odd(n_squared) {
// Accumulate value, if it's odd
acc += n_squared;
}
}
println!("imperative style: {}", acc);
// Functional approach
let sum_of_squared_odd_numbers: u32 =
(0..).map(|n| n * n) // All natural numbers squared
.take_while(|&n_squared| n_squared < upper) // Below upper limit
.filter(|&n_squared| is_odd(n_squared)) // That are odd
.fold(0, |acc, n_squared| acc + n_squared); // Sum them
println!("functional style: {}", sum_of_squared_odd_numbers);
}
Evolving a for loop in pascal …
for n in [0..99] do
begin
n_squared := n * n; // Square the number
if n_squared >= upper then // Break loop if exceeded the upper limit
break;
else if odd(n_squared) then // Accumulate value, if it's odd
acc := acc + n_squared;
end;
decomposing to composable functions …
function fn ( x:integer ) : integer;
begin
var predicate := (x < upper) and odd (x);
result := x * predicate.ToInteger;
end;
begin
for var n in [0..99] do acc := acc + fn(n²);
end.
Written more functionally … we write less code … and it can be parallelised …
map ( [0..99], fn(n²) ) // apply fn across input range
. sum // sum the results
Compare to the format of TParallel.For (System.Threading), which only allows a procedure : ![]()
TParallel.For(1, 10, procedure(i: integer)
begin
// …
end
);
Super short (2 mins) … pretty nice explanation that (for good or ill) steps aside from the theory or even discussing nullable types.
Well, Mr Bond … we meet again.
(2006) " The LINQ Project - .NET Language Integrated Query "
Don Box, Architect, Microsoft Corporation and
*** Anders Hejlsberg ***, Technical Fellow, Microsoft Corporation
The Bird–Meertens formalism (BMF) is a calculus for deriving programs from specifications by a process of equational reasoning. It was devised by Richard Bird and Lambert Meertens
It is sometimes referred to in publications as BMF, as a nod to Backus–Naur form.
Facetiously it is also referred to as Squiggol, as a nod to ALGOL, because of the “squiggly” symbols it uses.
Bird (1989) transforms inefficient easy-to-understand expressions (“specifications”) into efficient involved expressions (“programs”) by algebraic manipulation. For example, the specification “max . max sum . segs” is an almost literal translation of “maximum segment sum algorithm”,[5] but running that program on a list of size n will take time O(n^3) in general. From this, Bird computes an equivalent program that runs in time O(n), and is in fact a functional version of Kadane’s algorithm.
A point of great interest for this lemma is its application to the derivation of highly parallel implementations of computations. For any list homomorphism h , there exists a parallel implementation. That implementation cuts the list into chunks, which are assigned to different computers; each computes the result on its own chunk. It is those results that transit on the network and are finally combined into one. In any application where the list is enormous and the result is a very simple type – say an integer – the benefits of parallelisation are considerable.
This is the basis of the map-reduce approach.
Continuation-passing style
"CPS turns a program inside-out. In the process, the programmer may feel that his brain has been turned inside-out as well.
Why CPS? What exactly can a programmer do with CPS besides showoff at parties?
Compilers use a more thorough CPS transformation to produce an intermediate form amenable to many analyses. UI frameworks use CPS to keep the UI responsive while allowing nonlinear program interaction. Web servers use CPS to allow computation to flow asynchronously across pages.
Most programmers have used functions which take a callback. Often, the callback is the code that is invoked upon completion of the function. In these cases, the callback is an explicitly-passed continuation."
In “CUPID for joyful coding” (https://dannorth.net/cupid-for-joyful-coding/) …
Perl coined the acronym TIMTOWTDI—“there is more than one way to do it”—pronounced “Tim Toady”.
You can write functional, procedural, or object-oriented code in most of them, which creates a shallow learning curve from whichever language you know.
For something as simple as processing a sequence of values, most of these languages let you:
- use an iterator
- use an indexed for-loop
- use a conditional while-loop
- use a function pipeline with a collector (“map-reduce”)
- write a tail-recursive function
This means that in any non-trivial size of code, you will likely find examples of each of these, often in combination with each other. Again, this all adds cognitive load, impacting your capacity to think about the problem at hand, increasing uncertainty, and reducing joy.
Code idioms occur at all levels of granularity: naming functions, types, parameters, modules; layout of code; structure of modules; choice of tools; choice of dependencies; how you manage dependencies; and so on.
Wherever your technology stack lies on the spectrum of opinionatedness, the code you write will be more empathic and joyful if you take the time to learn the idioms of the language, its ecosystem, its community, and its preferred style.
… But on the other hand … idioms can develop over time. Eg inline variables, type inference, and range-for loops.




![Finding Nemo, or Evolution of a for Loop - Arseniy Zaostrovnykh [CppNow 2021]](https://img.youtube.com/vi/jXWz0kwtxrQ/maxresdefault.jpg)

